Cryptography Studies
cryptography (study I) from macumbista on Vimeo.
I took a quick break from some soundtracking work to build and document this little box over the weekend. I have been interested in examining the use of simple analog implementations of pseudo-random number generators, akin to those used in encryption algorithms, for the chaotic production of sound patterns. One of the simplest pseudo-random number generators is a three-stage shift register with a non-linear feedback loop, such as that found in Rob Hordijk’s “Benjolin” instrument design.
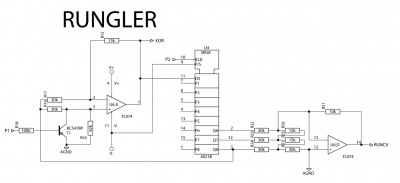
Rungler schematic courtesy of Rob Hordijk, redrawn by Casper Electronics
The most interesting part of the Benjolin is a circuit Hordijk calls a “rungler” (the rest of the Benjolin being two simple oscillators and a resonant filter). It is made up of a shift register in the middle (U4, a 4021B integrated circuit), an XOR (eXclusive OR) logic gate created by one transistor and an op-amp on the left, and finally a rudimentary Digital-to-Analog converter built around another op-amp on the right. Note the feedback from the last stage of the shift register to one input of the XOR, or what could be called the “poor man’s ring modulator”. The other XOR input comes from one of the two oscillators (P1).
Hordijk writes:
The purpose of the rungler is to create short stepped patterns of variable length and speed. […] It needs two frequency sources to work and basically creates a complex interference pattern that can be fed back into the frequency parameters of the driving oscillators to create an unlimited amount of havoc.
The rungler is basically a CMOS shift register clocked by one oscillator and receiving its data input from the other oscillator. The output bits of the shift register are used as […] a 3 bit code that is fed into a 3 bit DA converter. This DA eight level output voltage is fed back to the oscillator frequency control inputs. The output of the DA is the ‘rungler CV signal'[…]
When the rungler signal is fed back to the frequency parameters of the oscillators it will change the triangle waveforms and pulse widths of the oscillator outputs[…]
The rungler will try to find a balanced state. In this way it behaves according to principle from Chaos Theory. There seems to be an unlimited amount of possible balanced states and when a balanced state is just slightly disturbed it can be noted that it takes a little time to find the next balanced state, with noticeable bifurcations, etc.
Now, a shift register itself is a quite simple idea; one has several stages, and information (an analog voltage in some cases, or a binary state in others) gets passed from one stage to the next every time the shift register gets a clock signal. Passing the last stage of the shift register back to the first results in a loop, however any sort of transformation done to the last stage before it gets sent back to the first (an XOR “ring modulation” in the Benjolin’s case) means that each iteration of the loop changes. This satisfies the basic requirements of chaotic syntheses: that there is feedback, that there is nonlinearity and that there is sensitivity to initial conditions. (see Slater, Dan, “Chaotic Sound Synthesis”, Computer Music Journal 22.2 19 September 1998, pp 12-19.)
Not surprisingly, analog shift registers such as the one produced by Serge Tcherepnin were often referred to as “arabesque generators”, as in this image from Synapse Magazine September/October 1976. However, we could also refer to this structure as a Lindenmayer, or L-system. An L-system is essentially a grammatical system which rewrites itself for every new iteration according to a system of rules.
Here is Lindenmayer’s original L-system for modeling the growth of algae:
variables : A B
constants : none
start : A
rules : (A → AB), (B → A)
which produces:
n = 0 : A
n = 1 : AB
n = 2 : ABA
n = 3 : ABAAB
n = 4 : ABAABABA
n = 5 : ABAABABAABAAB
n = 6 : ABAABABAABAABABAABABA
n = 7 : ABAABABAABAABABAABABAABAABABAABAAB
(Source: Wikipedia)
In Non-Standard Sound Synthesis with L-Systems, Stelios Manousakis refers to non-propagative L-systems as being similar to cellular automata algorithms in that the data produced doesn’t branch out and expand endlessly, but rather is used as rules for determining the output of each cell. In our 3 stage shift register example, the non-linear feedback applied to the last stage before it returns to the first would be the new “grammatical rule” applied to the next iteration.
Now, another term we could use to describe a chaotically-produced series of binary numbers with a high sensitivity to the initial conditions (or “seed”) of the process which creates them is a Pseudo-Random Number Generator (also know as a Deterministic Random Bit Generator). And many implementations of a PRNG use what are called Linear Feedback Shift Registers to create those bits, which are the basic building blocks of many sorts of encryption processes.
Our 3-bit Benjolin is a far cry from the 128- and 256-bit encryption algorithms commonly used for digital security today (to say nothing of the “uncrackable” 1024-bit scheme used by the RSA algorithm), and probably bears a closer resemblance to the “shuffle” feature on my ITunes, which “randomly” seems to play back the same 220 songs out of the 22,000 in my MP3 collection. Or, as quantum mechanics pioneer John von Neumann joked, “Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin.” For the purpose of creating generative sound compositions in realtime, however, these pseudo-random bits appear to provide an interesting and “musical” balance between randomness and structure.
Other circuits or projects involving the potentially chaotic use of shift registers and/or pseudo-random number generators include the CGS 34 ASR (which is of course influenced by the original Serge ASR), the CGS 31 Digital Noise, the random voltage generator from the Buchla 208 “Music Easel” and the mighty Klee Sequencer.
As a footnote, I have to add that the man who first uttered the name “L-system” to me is the same man whose film is now sitting on my desktop, waiting to be scored. So with this musing on the cyclical nature of the universe, I bid you farewell for now.
Now Playing
drudkh–eternal turn of the wheel[2012 season of mist]
earth–angels of darkness demons of light II[2012 southern lord]
keith fullerton whitman–generators[2012 editions mego]
mirroring–foreign body[2012 kranky]
oren ambarchi–audience of one[2012 touch]
Cool post & I love your Benjolin Beatbox! I have to keep mine in a box on the shelf because I tend to get lost in it.
Just a minor note, the 4021 is actually an 8 stage shift register, its just that it only has 3 output bits.
One thing I’ve not seen mentioned in the disscussion of possible mods for the Rungler is the ability to ‘preset’ a pattern into the register which would then be “rungled” which may be of interest in connection to your cryptography investigations.
Interesting video, but I’m a bit confused. If this is a study in chaos, why do you frequently change the circuit by moving patch cords and knobs. I understand that the mind/body/universe system is itself chaotic, but the Benjolin is a nice self-contained chaotic system and enjoyable just to set it and forget it.
I’m not advocating that there is only one way to enjoy these systems. Human interaction is one of the best ways to make the output musical.
Anyway, very cool…
Hey Mosc, glad you could drop by! Think of it as a time-lapse study in the different patterns which could emerge. The Benjolin has a tendency to settle into a predictable state at some point in the iterations, so I tried to catch the moments before it did, as well as demonstrate the process I used to get there. Best wishes! Derek
[…] “Catjar in the Rye” (or “Betty”, as she is know to her friends) is an experimental sound instrument for Swedish composer Andreas Catjar. It combines a chaotic Benjolin synthesizer, extreme fuzz distortion unit and speaker-contact-mic-feedback system into one rugged flightcase. The Benjolin features several modifications, including patchable routing banana jacks, LED lights for the three stages of its analog shift register and an external audio input. My thanks go out to Rob Hordijk, who designed the Benjolin circuit, and to Pete Edwards/Casper Electronics for his help in working out the modifications. You can read a few of my thoughts on using analog shift registers for chaotic sound synthesis in this post. […]